El planeta Marte, en su movimiento alrededor del Sol, describe una órbita elíptica.
El punto de la órbita más cercano al Sol, perihelio, se encuentra a 206,7·106
km, mientras que el
punto de la órbita más alejado del Sol, afelio, está a 249,2·106
km. Si la velocidad de Marte en el
perihelio es de 26,50 km s-1, determine:
a) La velocidad de Marte en el afelio.
b) La energía mecánica total de Marte en el afelio.
Datos: Constante de Gravitación Universal, G = 6,67·10-11 N m2
kg-2; Masa de Marte, MM =
6,42·1023 kg; Masa del Sol MS = 1,99·1030 kg.
B.Pregunta 1.- Un astronauta utiliza un muelle de constante elástica k=327 N m-1 para determinar
la aceleración de la gravedad en la Tierra y en Marte. El astronauta coloca en posición vertical el
muelle y cuelga de uno de sus extremos una masa de 1 kg hasta alcanzar el equilibrio. Observa
que en la superficie de la Tierra el muelle se alarga 3 cm y en la de Marte sólo 1,13 cm.
a) Si el astronauta tiene una masa de 90 kg, determine la masa adicional que debe añadirse para
que su peso en Marte sea igual al de la Tierra.
b) Calcule la masa de la Tierra suponiendo que sea esférica.
Datos: Constante de Gravitación Universal, G = 6,67·10-11 N m2
kg-2; Radio de la Tierra, RT =
6,37·106
m.
martes, 31 de diciembre de 2019
lunes, 30 de diciembre de 2019
MADRID 2007. SEPTIEMBRE A. Problema 2.-
Tres hilos conductores rectilíneos, muy largos y
paralelos, se disponen como se muestra en la figura (perpendiculares
al plano del papel pasando por los vértices de un triángulo
rectángulo). La intensidad de corriente que circula por todos ellos es
la misma, I=25 A, aunque el sentido de la corriente en el hilo C es
opuesto al de los otros dos hilos. Determine:
a) El campo magnético en el punto P, punto medio del segmento AC.
b) La fuerza que actúa sobre una carga positiva Q=1,6×10-19 C si se encuentra en el punto P moviéndose con una velocidad de 106 m/s perpendicular al plano del papel y con sentido hacia fuera.
Dato: Permeabilidad magnética del vacío μo = 4π×10-7 N A-2
a) El campo magnético en el punto P, punto medio del segmento AC.
b) La fuerza que actúa sobre una carga positiva Q=1,6×10-19 C si se encuentra en el punto P moviéndose con una velocidad de 106 m/s perpendicular al plano del papel y con sentido hacia fuera.
Dato: Permeabilidad magnética del vacío μo = 4π×10-7 N A-2
domingo, 29 de diciembre de 2019
MADRID.2011.MODELO.B. Problema 2.-
Se hace girar una espira conductora circular de 5
cm de radio respecto a uno de sus diámetros en una región con un
campo magnético uniforme de módulo B y dirección perpendicular
a dicho diámetro. La fuerza electromotriz inducida (ε) en la espira) en la espira
depende del tiempo (t) como se muestra en la figura. Teniendo en
cuenta los datos de esta figura, determine:
a) La frecuencia de giro de la espira y el valor de B.
b) La expresión del flujo de campo magnético a través de la espira en función del tiempo.
a) La frecuencia de giro de la espira y el valor de B.
b) La expresión del flujo de campo magnético a través de la espira en función del tiempo.
sábado, 28 de diciembre de 2019
SEPTIEMBRE-2007.OPCIÓN-A
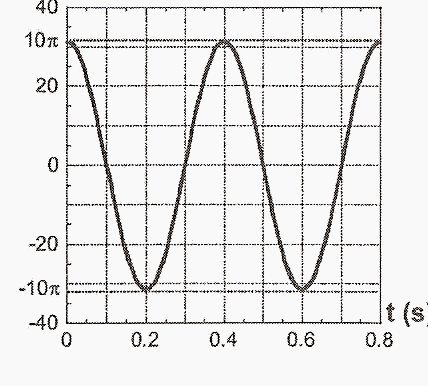 Una partícula de masa m = 20 g. Oscila armónicamente en la forma x(t) = A sen ωt. En la figura se representa la velocidad de la partícula en función del tiempo. Una partícula de masa m = 20 g. Oscila armónicamente en la forma x(t) = A sen ωt. En la figura se representa la velocidad de la partícula en función del tiempo.
|
viernes, 27 de diciembre de 2019
JUNIO-2007.OPCION-B
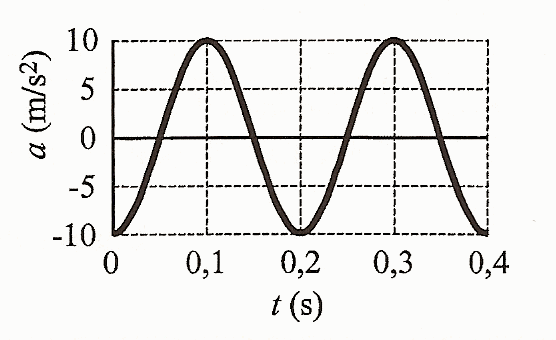 Un cuerpo de masa M = 0,1 kg oscila armónicamente en torno al origen O de un eje OX. En la figura se representa la aceleración de M en función del tiempo
Un cuerpo de masa M = 0,1 kg oscila armónicamente en torno al origen O de un eje OX. En la figura se representa la aceleración de M en función del tiempo- Determina la frecuencia y la amplitud de la oscilación de M
- Determina y representa gráficamente la energía cinética de M en función del tiempo.
jueves, 26 de diciembre de 2019
MADRID.2015-Junio-Coincidentes A. Pregunta 3.-
Considere un hilo rectilíneo muy largo dirigido a lo largo
del eje Y, por el que circula una intensidad de corriente I = 3 A. A una
distancia d = 1 m del hilo, una carga q = 5 μC se mueve inicialmente a laC se mueve inicialmente a la
velocidad ⃗v=20⃗j m s-1, tal y como se indica en la figura. Determine:
a) El valor del campo magnético ⃗B en el punto en el que se encuentra inicialmente la carga q y la fuerza que ésta experimenta.
b) La carga que habría que situar en ( d 2 ,0,0) para compensar la fuerza magnética que ejerce el hilo sobre q en el mismo instante inicial.
Datos: Permeabilidad magnética del vacío, μ0 = 4π·10-7 N A-2.; Constante de la Ley de Coulomb, K = 9·109 N m2 C-2 .
a) El valor del campo magnético ⃗B en el punto en el que se encuentra inicialmente la carga q y la fuerza que ésta experimenta.
b) La carga que habría que situar en ( d 2 ,0,0) para compensar la fuerza magnética que ejerce el hilo sobre q en el mismo instante inicial.
Datos: Permeabilidad magnética del vacío, μ0 = 4π·10-7 N A-2.; Constante de la Ley de Coulomb, K = 9·109 N m2 C-2 .
miércoles, 25 de diciembre de 2019
MADRID,2019-Junio-Coincidentes B. Pregunta 3.-
Una bobina circular está formada por un hilo conductor de 25 cm de longitud que
se enrolla en 5 vueltas, y cuya resistencia total es de 10 Ω. La bobina está situada en el plano xy
con su centro en el origen de coordenadas cartesiano. En la región hay un campo magnético
variable en el tiempo
Calcule en el instante t = 0,25 s:
a) El flujo magnético a través de la bobina.
b) La fuerza electromotriz y la corriente eléctrica inducidas en la bobina
Calcule en el instante t = 0,25 s:
a) El flujo magnético a través de la bobina.
b) La fuerza electromotriz y la corriente eléctrica inducidas en la bobina
martes, 24 de diciembre de 2019
MADRID 2002. JUNIO
Cuestión 1.- Un planeta esférico tiene un radio de 3000 km, y la aceleración de la gravedad en su
superficie es 6 m/s2
.
A) ¿Cuál es su densidad media?
b) ¿Cual es la velocidad de escape para un objeto situado en la superficie de este planeta?
Dato: Constante de Gravitación Universal: G = 6,67x 10-11 N m2 kg-2 A.
Problema 1.- La velocidad angular con la que un satélite describe una órbita circular en torno al planeta Venus es ω1=1,45x10-4 rad/s y su momento angular respecto al centro de la órbita es L1=2,2x1012 kg m2 s-1
a) Determine el radio r1 de la órbita del satélite y su masa.
b) ¿Qué energía sería preciso invertir para cambiar a otra órbita circular con velocidad angular ω2=10-4 rad/s?
Datos: Constante de Gravitación Universal: G = 6,67x 10-11 N m2 kg-2 Masa de Venus: MV=4,87x 1024 kg
A) ¿Cuál es su densidad media?
b) ¿Cual es la velocidad de escape para un objeto situado en la superficie de este planeta?
Dato: Constante de Gravitación Universal: G = 6,67x 10-11 N m2 kg-2 A.
Problema 1.- La velocidad angular con la que un satélite describe una órbita circular en torno al planeta Venus es ω1=1,45x10-4 rad/s y su momento angular respecto al centro de la órbita es L1=2,2x1012 kg m2 s-1
a) Determine el radio r1 de la órbita del satélite y su masa.
b) ¿Qué energía sería preciso invertir para cambiar a otra órbita circular con velocidad angular ω2=10-4 rad/s?
Datos: Constante de Gravitación Universal: G = 6,67x 10-11 N m2 kg-2 Masa de Venus: MV=4,87x 1024 kg
lunes, 23 de diciembre de 2019
MADRID.2019-Julio-Coincidentes A. Pregunta 3.-
Una espira cuadrada, de lado a = 10
cm y resistencia R = 12 Ω, está inmersa en una región
del espacio en la que hay un campo magnético
uniforme B0 = 0,3 T. Determine:
a) La fuerza electromotriz inducida y la corriente que se induce, si la espira gira con velocidad angular constante de 10 rpm respecto de un eje que pasa por su centro y es paralelo a dos de sus lados y el campo magnético es perpendicular al eje de giro (ver figura a).
b) El vector fuerza que actúa sobre cada uno de las lados si el campo magnético es paralelo al eje de giro, la espira está en reposo y circula por ella una corriente de I = 0,5 A (ver figura b).
a) La fuerza electromotriz inducida y la corriente que se induce, si la espira gira con velocidad angular constante de 10 rpm respecto de un eje que pasa por su centro y es paralelo a dos de sus lados y el campo magnético es perpendicular al eje de giro (ver figura a).
b) El vector fuerza que actúa sobre cada uno de las lados si el campo magnético es paralelo al eje de giro, la espira está en reposo y circula por ella una corriente de I = 0,5 A (ver figura b).
domingo, 22 de diciembre de 2019
MADRID.2020-Modelo
A. Pregunta 1.- El satélite UARS se puso en órbita en 1991 para estudiar la entrada y salida de
energía en la atmósfera superior. Su masa era de 5800 kg y realizaba 15 órbitas diarias. En 2005,
el satélite se quedó sin combustible y dejó de operar. Calcule:
a) La altura sobre la superficie de la Tierra de dicho satélite cuando estaba en órbita.
b) La energía total del satélite cuando estaba en órbita.
Datos: Constante de Gravitación Universal, G = 6,67·10-11 N m2 kg-2; Radio de la Tierra, RT = 6371 km; Masa de la Tierra, MT = 5,97·1024 kg.
B. Pregunta 1.-. Unos astrónomos han descubierto un nuevo sistema solar, formado por una estrella de masa 6,0·1030 kg, que desempeña el papel del sol, y un planeta que gira en torno a ella en una órbita circular, tardando 3 años terrestres en dar una vuelta completa.
a) Determine la distancia a la que se encuentra el planeta del sol.
b) Si en la superficie del planeta la aceleración de la gravedad es 15 m s-2 y la velocidad de escape es de 11,2 km s-1, ¿cuánto valen la masa y el radio del planeta?
Dato: Constante de Gravitación Universal, G = 6,67·10-11 N m2 kg-2 .
a) La altura sobre la superficie de la Tierra de dicho satélite cuando estaba en órbita.
b) La energía total del satélite cuando estaba en órbita.
Datos: Constante de Gravitación Universal, G = 6,67·10-11 N m2 kg-2; Radio de la Tierra, RT = 6371 km; Masa de la Tierra, MT = 5,97·1024 kg.
B. Pregunta 1.-. Unos astrónomos han descubierto un nuevo sistema solar, formado por una estrella de masa 6,0·1030 kg, que desempeña el papel del sol, y un planeta que gira en torno a ella en una órbita circular, tardando 3 años terrestres en dar una vuelta completa.
a) Determine la distancia a la que se encuentra el planeta del sol.
b) Si en la superficie del planeta la aceleración de la gravedad es 15 m s-2 y la velocidad de escape es de 11,2 km s-1, ¿cuánto valen la masa y el radio del planeta?
Dato: Constante de Gravitación Universal, G = 6,67·10-11 N m2 kg-2 .
sábado, 21 de diciembre de 2019
MADRID.2017-Septiembre A. Pregunta 3.-
Dos cargas de +5 nC están separadas una distancia
de 4 cm de acuerdo a la figura adjunta. Calcule:
a) El campo eléctrico en el punto A y en el punto B creado por ambas cargas.
b) El potencial eléctrico en el punto A y en el punto B, y el trabajo que hay que realizar sobre una carga de +3 nC para desplazarla desde el punto A al punto B. Dato: Constante de la Ley de Coulomb, K = 9·109 N m2 C-2
a) El campo eléctrico en el punto A y en el punto B creado por ambas cargas.
b) El potencial eléctrico en el punto A y en el punto B, y el trabajo que hay que realizar sobre una carga de +3 nC para desplazarla desde el punto A al punto B. Dato: Constante de la Ley de Coulomb, K = 9·109 N m2 C-2
viernes, 20 de diciembre de 2019
MADRID 2016-Modelo B. Pregunta 2.-
Una masa puntual de 2 g unida a un muelle de masa despreciable se mueve con
una velocidad dada por la expresión: v (t)=5sen(
π
2
t+
3π
2 )cm s
−1
. Determine:
a) La amplitud de oscilación y la fase inicial del movimiento.
b) Las energías cinética y potencial en el instante t = 1s.
a) La amplitud de oscilación y la fase inicial del movimiento.
b) Las energías cinética y potencial en el instante t = 1s.
jueves, 19 de diciembre de 2019
MADRID. 2018-Junio-coincidentes A. Pregunta 2.-
Una onda transversal se
propaga en el sentido positivo del eje x. En las
figuras se muestran: la variación de la
elongación en un instante t = 0 a lo largo del eje
x y la elongación del punto de coordenada x = 0
en función del tiempo.
Determine:
a) La longitud de onda y la frecuencia.
b) La expresión matemática de la onda.
Determine:
a) La longitud de onda y la frecuencia.
b) La expresión matemática de la onda.
SEPTIEMBRE 2013. OPCIÓN A
Una onda transversal se propaga de izquierda a derecha, según el eje OX, a lo largo de una cuerda horizontal tensa e indefinida, siendo su longitud de onda λ = 10 cm. La onda está generada por un oscilador que vibra, en la dirección del eje OY, con un movimiento armónico simple de frecuencia f = 100 Hz y amplitud A = 5 cm. En el instante inicial t = 0, el punto x = 0 de la cuerda tiene elongación nula.
a) Escribir una expresión matemática de la onda indicando el valor numérico de todos los parámetros (en unidades S.I.). Escribir la ecuación que describe el movimiento de un punto situado a 30 cm a la derecha del origen.
b) Determinar la velocidad de propagación de la onda y la velocidad máxima de oscilación de un punto cualquiera de la cuerda.
c) Dibujar un esquema de la cuerda en una longitud de 20 cm, en el instante t = 0
|
SEPTIEMBRE 2014. OPCIÓN B
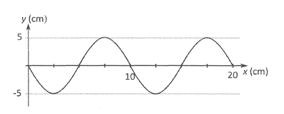 Por una cuerda tensa se propaga, en el sentido positivo del eje X, una onda sinusoidal transversal. Los puntos de la cuerda oscilan con una frecuencia f = 2 Hz. En la gráfica se representa la posición de los puntos de la cuerda en el instante t = 0. Por una cuerda tensa se propaga, en el sentido positivo del eje X, una onda sinusoidal transversal. Los puntos de la cuerda oscilan con una frecuencia f = 2 Hz. En la gráfica se representa la posición de los puntos de la cuerda en el instante t = 0.
a) Determine la amplitud de la onda, su longitud de onda y la velocidad de propagación de la onda.
b) Calcule la máxima velocidad de oscilación transversal de los puntos de la cuerda.
c) Escriba la función de onda correspondiente, en unidades S.I.
|
JUNIO 2017. OPCIÓN A
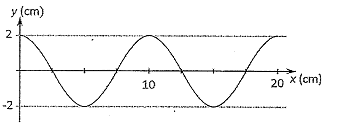
Por una cuerda tensa se propaga, en el sentido positivo del eje x, una onda armónica transversal. Los puntos de la cuerda oscilan con una frecuencia f = 4 Hz. En la gráfica se representa la posición de los puntos de la cuerda en el instante t = 0.
a) Determine la longitud de onda y la velocidad de propagación de la onda.
b) Escriba la función de onda correspondiente, en unidades S.I.
c) Calcule la máxima velocidad de oscilación trasversal de los puntos de la cuerda.
|
MADRID. 2020-Modelo A. Pregunta 2.-
Una onda armónica unidimensional se propaga
a lo largo del sentido positivo del eje x con una velocidad de
propagación de 1500 m s-1, donde la gráfica adjunta muestra la
elongación de la onda para el instante t = 0 s.

a) Determine el número de onda y la frecuencia angular de
dicha onda.
b) Obtenga la expresión matemática que represente dicha
onda.
martes, 17 de diciembre de 2019
MADRID. 2009-Modelo Problema 1.-
En la figura se muestra la representación gráfica de la energía potencial (EP) de un
oscilador armónico simple constituido por una masa puntual de valor
200 g unida a un muelle horizontal, en función de su elongación (x).
a) Calcule la constante elástica del muelle
b) Calcule la aceleración máxima del oscilador.
c) Determine numéricamente la energía cinética cuando la masa está en la posición x = +2,3 cm.
d) ¿Dónde se encuentra la masa puntual cuando el módulo de su velocidad es igual a la cuarta parte de su velocidad máxima?
a) Calcule la constante elástica del muelle
b) Calcule la aceleración máxima del oscilador.
c) Determine numéricamente la energía cinética cuando la masa está en la posición x = +2,3 cm.
d) ¿Dónde se encuentra la masa puntual cuando el módulo de su velocidad es igual a la cuarta parte de su velocidad máxima?
MADRID. 2014-Junio-Coincidentes B. Pregunta 2.-
Una objeto de 100 g de masa describe un movimiento armónico simple a lo largo
del eje X, en torno a x = 0. Cuando el objeto se encuentra en el origen de coordenadas, el módulo
de su velocidad es 4 m s-1 y cuando está en el punto x = +40 cm es de 2 m s-1. Calcule:
a) La energía mecánica y la amplitud del movimiento.
b) La aceleración de la partícula en x = +40 cm y su periodo de oscilación.
a) La energía mecánica y la amplitud del movimiento.
b) La aceleración de la partícula en x = +40 cm y su periodo de oscilación.
MADRID. 2010-Junio-Coincidentes A. Cuestión 1.-
La gráfica muestra el desplazamiento
horizontal x=x(t) respecto del equilibrio de una masa de
0,5 kg unida a un muelle.
a) Obtenga la constante elástica del muelle.
b) Determine las energías cinética y potencial del sistema en el instante t = 0,25 s.
a) Obtenga la constante elástica del muelle.
b) Determine las energías cinética y potencial del sistema en el instante t = 0,25 s.
viernes, 13 de diciembre de 2019
SEPTIEMBRE 2006. OPCIÓN B
La bolita de un péndulo simple realiza una oscilación aproximadamente horizontal y armónica, ( presencia del campo gravitatorio terrestre, con un periodo T = 2 s y una amplitud A = 5 cm.
|
JUNIO 2013. OPCIÓN A
Una masa m unida a un muelle realiza un movimiento armónico simple. La figura representa su energía potencial en función de la elongación x.
a) Representar la energía cinética y la energía total en función de x.
b) Calcular la constante elástica del muelle.
c) Si la masa es m = 1 kg, calcular su velocidad máxima. ¿en qué punto x se alcanza esta velocidad?
SEPTIEMBRE 2015. OPCIÓN A
Dos partículas de masas m y 4m oscilan en un movimiento armónico simple; cada una de ellas está sujeta al extremo de un muelle horizontal de constante K. Calcule:
a) El cociente entre los periodos de oscilación de las dos partículas.
b) El cociente entre las energías potenciales máximas de las dos partículas cuando ambas oscilan con la misma amplitud A.
c) La velocidad máxima que alcanza la masa m.
Datos: K = 80 N/m, m = 2 kg, A = 0,5 m
|
JUNIO 2018. OPCIÓN A
Una partícula de masa m = 10 g oscila armónicamente a lo largo del eje OX en la forma x = A senωt con A = 0,2 m y ω = 10π rad∙s-1.
- Determine y represente gráficamente la fuerza que actúa sobre la partícula en función del tiempo para dos periodos completos de la oscilación.
- Calcule la energía mecánica de la partícula.
- Determine y represente gráficamente la energía cinética de m en función del tiempo para dos periodos completos de la oscilación.
SEPTIEMBRE 2018. OPCIÓN B
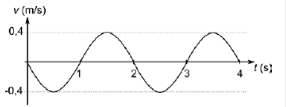 Una masa m = 100 g oscila armónicamente colgada del extremo de un muelle. La velocidad de la masa en función del tiempo se representa en la gráfica. Una masa m = 100 g oscila armónicamente colgada del extremo de un muelle. La velocidad de la masa en función del tiempo se representa en la gráfica.
|
jueves, 12 de diciembre de 2019
MADRID. 2015 Junio A. Pregunta 2.
Un muelle de masa despreciable y de longitud 5 cm cuelga del techo de una casa
en un planeta diferente a la Tierra. Al colgar del muelle una masa de 50 g, la longitud final del
muelle es 5,25 cm. Sabiendo que la constante elástica del muelle es 350 N m-1:
a) Determine el valor de la aceleración de la gravedad en la superficie del planeta.
b) El muelle se separa con respecto a su posición de equilibrio 0,5 cm hacia abajo y a continuación es liberado. Determine, la ecuación que describe el movimiento de la masa
que cuelga del muelle.
martes, 10 de diciembre de 2019
JUNIO 2015. OPCIÓN B
Una masa m oscila sujeta al extremo de un muelle horizontal de constante elástica K = 50 N/m con un periodo de oscilación T = 4 s.
a) Calcule la masa mb) Calcule la amplitud máxima A para que la aceleración de la masa no supere amax = 2 m/s2. Calcule la velocidad máxima para dicha amplitud.c) En t = 0 la masa m se separa una distancia x0 = A hacia la derecha y se suelta con velocidad nula. Escriba la ecuación de la posición de m en función del tiempo en unidades S.I. Represéntela gráficamente para dos periodos de oscilación.
JUNIO 2016. OPCIÓN B
a) Escriba la ecuación de la elongación de un movimiento armónico simple y comente el significado físico de las magnitudes que aparecen en dicha ecuación.
Un bloque de masa M =0,4 kg desliza sobre una superficie horizontal sin rozamiento sujeto al extremo de un muelle horizontal de constante elástica k = 10 N/m. Cuando pasa por la posición de equilibrio del sistema masa-muelle lleva una velocidad v0 = 1 m/s.
b) Calcule la frecuencia y la amplitud de las oscilaciones de M.
c) Determine la posición del centro de M en función del tiempo, x(t), a partir del instante (t = 0) en que pasa por la posición de equilibrio (x = 0) moviéndose hacia la derecha. Represente gráficamente x(t) para dos periodos de oscilación.
|
SEPTIEMBRE 2017. OPCIÓN B
a) Escribe la función que describe la elongación de un movimiento armónico simple y comenta el significado físico de las magnitudes que aparecen en dicha función.
Un bloque de masa M = 0,4 kg desliza sobre una superficie horizontal sin rozamiento sujeto al extremo de un muelle horizontal. La amplitud del movimiento es A = 20 cm y la elongación en el instante inicial es x = -20 cm. La energía total es 2 J. Calcule:
b) La constante elástica del resorte.
c) La función que describe el movimiento del bloque.
|
miércoles, 4 de diciembre de 2019
JUNIO 99. OPCIÓN B (repaso electrostática)
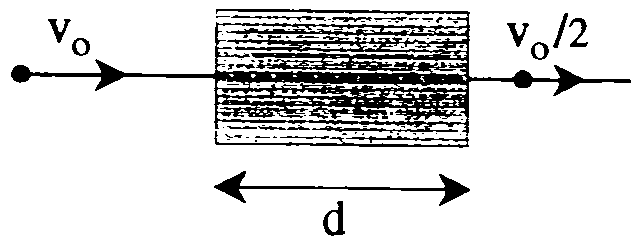 Un electrón con energía cinética inicial 100 eV penetra en la región sombreada de la figura, de anchura d = 10 cm, donde se sabe que existe un campo eléctrico uniforme. Se observa que el electrón atraviesa dicha región sin desviarse de su trayectoria rectilínea inicial, pero su velocidad a la salida es la mitad de la inicial. Calcula: Un electrón con energía cinética inicial 100 eV penetra en la región sombreada de la figura, de anchura d = 10 cm, donde se sabe que existe un campo eléctrico uniforme. Se observa que el electrón atraviesa dicha región sin desviarse de su trayectoria rectilínea inicial, pero su velocidad a la salida es la mitad de la inicial. Calcula:
|
martes, 3 de diciembre de 2019
MADRID. 2007. MODELO A. PROBLEMA 2.
En el circuito de la figura la varilla MN se mueve con
una velocidad constante de valor v = 2 m/s en dirección perpendicular
a un campo magnético uniforme de valor 0,4 T. Sabiendo que el valor
de la resistencia R es 60 Ω y que la longitud de la varilla es 1,2 m:
a) Determine la fuerza electromotriz inducida y la intensidad de la
corriente que circula en el circuito.
b) INTERESANTE Si a partir de un cierto instante (t = 0) la varilla se frena con aceleración constante hasta pararse
en 2 s, determine la expresión matemática de la fuerza electromotriz inducida en función del
tiempo, en el intervalo de 0 a 2 segundos.
*pista: x=x0+v0t+1/2at2
MADRID. 2012. MODELO B. PREGUNTA 5
Se tiene el circuito de la figura en forma de triángulo
rectángulo, formado por una barra conductora vertical que se desliza
horizontalmente hacia la derecha con velocidad constante v = 2,3 m/s
sobre dos barras conductoras fijas que forman un ángulo α = 45º.
Perpendicular al plano del circuito hay un campo magnético uniforme y
constante B = 0,5 T cuyo sentido es entrante en el plano del papel. Si
en el instante inicial t = 0 la barra se encuentra en el vértice izquierdo
del circuito:
a) Calcule la fuerza electromotriz inducida en el circuito en el instante
de tiempo t = 15 s.
b) Calcule la corriente eléctrica que circula por el circuito en el instante
t = 15 s, si la resistencia eléctrica total del circuito en ese instante es 5 Ω. Indique el sentido en el
que circula la corriente eléctrica.
MADRID. 2018. MODELO B. PREGUNTA 3.
Una varilla conductora puede deslizar sin rozamiento a lo largo de dos alambres
conductores paralelos, separados una distancia de L = 5 cm, que cierran un circuito a través de
una resistencia de R = 150 Ω. Este circuito forma una
espira cerrada que se encuentra inmersa en un
campo magnético uniforme, tal y como se muestra en
la figura adjunta. Inicialmente la varilla se encuentra a
una distancia d = 10 cm de la resistencia. Calcular
para el instante t = 0,2 s el flujo magnético que
atraviesa la espira y la corriente que circula por ella
en los siguientes casos:
a) El campo magnético es constante e igual a 20 mT
y la varilla se desplaza hacia la derecha con una
velocidad de 4 m/s.
b) La varilla está inmóvil y el campo magnético varía con el tiempo de la forma B = 5 t^3
(B
expresado en teslas y t en segundos).
MADRID. 2000-Modelo Cuestión 4.-
a) ¿Qué es un transformador? ¿Por qué son útiles para el transporte de la energía
eléctrica?
b) Si el primario de un transformador tiene 1200 espiras y el secundario 100, ¿qué tensión habrá que aplicar al primario para tener en la salida del secundario 6 V?
b) Si el primario de un transformador tiene 1200 espiras y el secundario 100, ¿qué tensión habrá que aplicar al primario para tener en la salida del secundario 6 V?
MADRID. 2003-Modelo Cuestión 4.-
Para transformar el voltaje de 220 V de la red eléctrica a un voltaje de 12 V que
necesita una lámpara halógena se utiliza un transformador:
a) ¿Que tipo de transformador debemos utilizar? Si la bobina del primario tiene 2200 espiras ¿cuántas espiras debe tener la bobina del secundario?
b) Si la lámpara funciona con una intensidad de corriente de 5 A ¿cuál es el valor de la intensidad de la corriente que debe circular por la bobina del primario?
a) ¿Que tipo de transformador debemos utilizar? Si la bobina del primario tiene 2200 espiras ¿cuántas espiras debe tener la bobina del secundario?
b) Si la lámpara funciona con una intensidad de corriente de 5 A ¿cuál es el valor de la intensidad de la corriente que debe circular por la bobina del primario?
SEPTIEMBRE 1996. OPCIÓN B
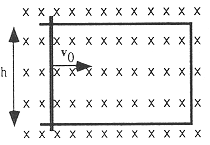 La figura muestra un rectángulo de alambre de altura h, situado en el plano del papel. El lado vertical izquierdo es móvil y se desliza horizontalmente hacia la derecha a velocidad constante v0, haciendo contacto permanentemente con los lados horizontales. En todo el espacio de este experimento hay un campo magnético uniforme B, perpendicular al papel, dirigido hacia adentro y representado por el símbolo x. La figura muestra un rectángulo de alambre de altura h, situado en el plano del papel. El lado vertical izquierdo es móvil y se desliza horizontalmente hacia la derecha a velocidad constante v0, haciendo contacto permanentemente con los lados horizontales. En todo el espacio de este experimento hay un campo magnético uniforme B, perpendicular al papel, dirigido hacia adentro y representado por el símbolo x.
|
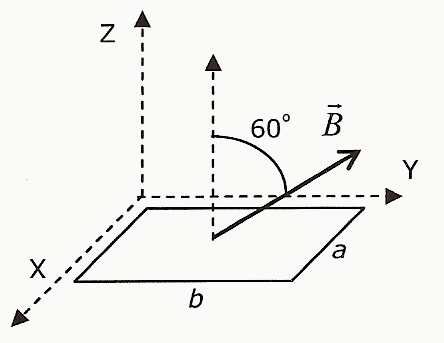
JUNIO 2010. OPCIÓN A
|
SEPTIEMBRE 2010. OPCIÓN A
|
JUNIO 2014. OPCIÓN A
a) Enunciar y explicar las leyes de Faraday y Lenz sobre inducción electromagnética.
b) Una bobina formada por 1000 espiras circulares de radio R = 10 cm está situada en una región en la que se encuentra un campo magnético de intensidad B = 0,01 T, perpendicular al plano de las espiras y dirigido hacia el norte, Calcular la f.e.m. media inducida en la bobina si el campo se duplica en un intervalo de tiempo Δt = 0,2 s. Indicar y justificar en qué sentido circulará la corriente por las espiras.
|
SEPTIEMBRE 2015. OPCIÓN A
a)
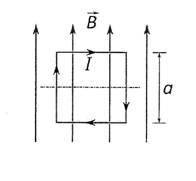 Enuncie y explique las leyes de Faraday y Lenz sobre inducción electromagnética. Enuncie y explique las leyes de Faraday y Lenz sobre inducción electromagnética.
En el seno de un campo magnético uniforme, de valor B = 10 mT, se sitúa una espira cuadrada rígida, de lado a = 10 cm (ver figura).
b) Calcule la fuerza (módulo, dirección y sentido) ejercida sobre cada uno de los lados de la espira cuando circula por ella una intensidad de corriente I = 2 A en el sentido indicado en la figura.
c) Determine el valor máximo de la fuerza electromotriz inducida en la espira cuando la hacemos rotar, alrededor de su eje de simetría horizontal, con una velocidad angular ω = 2π rad/s.
|
Suscribirse a:
Entradas (Atom)











