a) Enuncie y explique la Ley de desintegración exponencial radiactiva.
Un gramo de unos restos óseos contiene 9,5 x 108 átomos de carbono 14 (C-14). El análisis de una muestra actual de características similares revela que en el momento de la muerte de los animales los huesos tenían 6,9 x 109 átomos de C-14 por cada gramo.
b) Calcule la constante de desintegración y determine la antigüedad de los restos si sabemos que el período de semidesintegración del C-14 es de 5730 años.
a) Enuncia y explica la Ley de desintegración exponencial radiactiva. b) Para realizar una tomografía de emisión de positrones (PET) a un paciente, se inyecta un contraste con 18F, que es un isótopo radiactivo. Este isótopo del flúor tiene un periodo de semidesintegración de 76,1 minutos. ¿Al cabo de cuánto tiempo quedará en el organismo del paciente sólo el 10% de la cantidad inicial? |
a) Define las siguientes magnitudes asociadas a los procesos de desintegración radiactiva: Actividad radiactiva (A), periodo de semidesintegración (T) y vida media (τ). b) El tritio |
a) Explique qué es la fusión nuclear. ¿Cuál es la diferencia básica entre fusión y fisión nuclear? b) Uno de los procesos que utilizan las estrellas para convertir hidrógeno en helio es el denominado ciclo de carbono. La reacción nuclear viene dada por
Calcule la energía que se genera a partir de 1 kg de Datos: m( |
Explica brevemente qué es la fusión nuclear.
Calcula la energía que se libera en el siguiente proceso de fusión nuclear, expresando el resultado en Julios y MeV.
Las masas de los núcleos de Hidrógeno, Deuterio y Tritio son, respectivamente: 1,007825 u, 2,014102 u y 3,016049; 1 u = 1,66·10-27 kg; e = 1,6·10-19 C ; c = 3,00·108 m/s
Enuncia el principio de incertidumbre de Heisenberg y aplícalo a una bola de 100 g de masa que se mueve a 30 m/s si hemos medido su velocidad con una exactitud del 0,1 %.
Dato: Constante de Planck: h = 6,626·10-34 J.s
a) Enuncia y explica la hipótesis de De Broglie. b) Un electrón se acelera de forma que adquiere una energía cinética de 980 eV. ¿Cuál es la longitud de onda asociada al electrón? c) Si se desea frenar el electrón, ¿a qué diferencia de potencial electrostático habrá que someterlo? Haz un dibujo mostrando hacía dónde se desplaza el electrón y las dos placas, positiva y negativa, entre las que se introduce la diferencia de potencial electrostático. Datos: constante de Planck: h = 6,63·10-34 J·s; carga del electrón: qe = -1,60·10-19 C; masa del electrón: me = 9,1·10-31 kg; 1 eV = 1,60·10-19 J. |
a) Escriba la ecuación de De Broglie y comente su significado e importancia física.
b) Se lanza un electrón a una velocidad de 2,04·106 km/h, calcule su energía cinética y su longitud de onda asociada.
Datos: Masa del electrón: 9,1·10-31 kg; Constante de Planck: 6,626·10-34 J·s.
c) Un láser de He-Ne emite fotones de longitud de onda igual a 632,8 nm. Calcule la frecuencia de cada fotón y la energía asociada.
Datos: Velocidad de la luz: 3·108 m/s; Constante de Planck: 6,626·10-34 J·s
Ahora ya podéis empezar a resolver exámenes de Evau al completo, como este:
EXAMEN EVAU. JUNIO 2010
a) Defina el trabajo de extracción (o función trabajo) de un material y el potencial de frenado, enmarcando ambos conceptos dentro del efecto fotoeléctrico. b) Se tiene un metal cuyo trabajo de extracción o función trabajo es de 4 eV, calcule la mínima frecuencia de la luz con la que se conseguiría arrancar electrones del metal. Si se ilumina con una frecuencia doble de la obtenida, ¿cuál sería el potencial de frenado de los electrones? Datos: 1 eV = 1,6·10-19 J; velocidad de la luz: 3·108 m/s; constante de Planck: 6,626·10-34 J·s. |
a) Explique en qué consiste el efecto fotoeléctrico. ¿Qué es la frecuencia umbral? b) Iluminamos una muestra con radiación de longitud de onda λ = 23,7 x 10-9 m. Los fotoelectrones analizados tienen una energía cinética máxima de 47,7 eV. Calcule la función de trabajo (o trabajo de extracción) del material analizado en J y en eV. c) Determine la frecuencia umbral para este material. ¿Cómo cambiaría esta frecuencia umbral si se duplicase la intensidad del haz de radiación UV? Datos: c = 3,00 x 108 m/s; h = 6,63 x 10-34 J·s; 1 eV= 1,602 x 10-19 J |
Resuelve este examen de EvAU a excepción de la pregunta 7
EXT.EVAU 2021
Disponemos de una lente cuya distancia focal imagen es f’ = -20 cm. a) Calcule la potencia de la lente. b) Determine la posición y tamaño de la imagen de un objeto de 5 cm de altura cuando se coloca a 30 cm de la lente. c) Compruebe gráficamente sus resultados mediante un trazado de rayos |
Un sistema óptico está formado por dos lentes. La situada más a la izquierda es una lente convergente de distancia focal 20 cm, mientras que la segunda, situada a 100 cm de la primera, es una lente divergente de distancia focal 10 cm. Si situamos un objeto de altura 3 mm a 30 cm a la izquierda de la primera lente:
a) Deduzca la posición y tamaño de la imagen obtenida por el sistema.
b) Realice el correspondiente trazado de rayos de la formación de la imagen.
La lente de una máquina fotocopiadora se utiliza para capturar la imagen de una hoja situada a 20 cm de distancia de la lente, de forma que la imagen que se forma sobre el sensor de la fotocopiadora es invertida y del mismo tamaño que el objeto.
a) ¿A qué distancia del objetivo debemos colocar el sensor? Calcule la focal imagen que debe tener la lente. ¿Debe ser una lente convergente o divergente?
b) Compruebe gráficamente los resultados mediante un trazado de rayos.
Disponemos de una lente divergente de focal f’ = - 30 cm, a) Determina la posición y el tamaño de la imagen de un objeto de 2,5 cm de altura situado a 50 cm de la lente y haz un trazado de rayos del problema. b) ¿Cuál es la potencia de la lente? |
a) Explica cuál debe ser la posición de un objeto respecto a una lente delgada convergente para obtener una imagen virtual y derecha. Justifícalo gráficamente mediante un trazado de rayos. b) Un objeto de 1 cm de altura se sitúa a 8 cm delante de una lente convergente de 10 cm de distancia focal. Determina la posición, tamaño y tipo (real o virtual) de la imagen formada. |
Se desea capturar una imagen de un objeto situado a 80 cm usando una lente delgada convergente de distancia focal f’=120 mm. a) Haz un trazado de rayos de la lente, un objeto y su imagen en el que queden claramente dibujados y anotados todos los elementos y distancias involucradas. b) ¿A qué distancia de la lente se formará la imagen del objeto? c) Si la altura del objeto es de 15 cm, ¿Cuál será su altura en el plano imagen? |
Los espejos de garaje producen siempre una imagen derecha de los objetos, independientemente de su posición respecto del espejo. a) ¿Qué tipo de espejo es, convexo o cóncavo? Justifique su respuesta mediante trazado de rayos. b) Calcule el radio de curvatura de un espejo que permite observar la imagen de un coche, colocado a 3 m de distancia delante del espejo, con la mitad de tamaño que el objeto. |
Se dispone de un espejo cóncavo de focal 80 mm extraído de un pequeño telescopio.
a) Muestra mediante un trazado de rayos, dónde se formará la imagen de un objeto situado a 15 cm del vértice del espejo y de qué tipo será: ¿real o virtual?; ¿derecha o invertida?
b) ¿Qué aumento proporcionará el espejo con el objeto a la citada distancia?
c) Si sustituimos el espejo cóncavo por uno convexo con la misma focal, ¿Cuál sería el resultado del apartado b)?
Un haz de luz incide en la superficie de separación entre aire y aceite con un ángulo de 30o. Si el ángulo del rayo que penetra en el aceite es de 21o, a) Determina el índice de refracción del aceite. b) Explica el significado físico del índice de refracción. c) Si debajo del aceite hay agua (nagua=1,33), ¿Con qué ángulo se refractará? |
|
|
|
Responde a las siguientes preguntas: a) Explica que es la intensidad y el tono de una onda sonora. Indica sus unidades. Se desea construir un instrumento de viento cuya frecuencia fundamental sea f =174,6 Hz. Si se comporta como un tubo con un extremo cerrado y uno abierto, b) ¿Cuál debe ser su longitud? Dibuja el tubo y la onda estacionaria en su interior. Suponer la velocidad del sonido 340 m/s. c) Dibuja el siguiente armónico que se formaría en el tubo y obtén su longitud de onda. |
a) Se desea fabricar un instrumento musical de viento con una tubería de PVC. Para ello se corta la tubería en trozos de distintos tamaños con los dos extremos abiertos. Si el primer trozo tiene una longitud de 25 cm, calcule la frecuencia del armónico fundamental que producirá. ¿De qué tamaño habrá que cortar el siguiente trozo para que produzca una onda estacionaria cuya frecuencia del armónico fundamental sea 2/3 de la frecuencia del armónico fundamental del primer tubo? Dé la longitud de onda de ambos sonidos. Datos: Velocidad del sonido en el aire: 346 m/s.
b) Un barco se aproxima al puerto haciendo sonar su sirena, de 500 W de potencia. El aparato con el que se detecta el sonido tiene un umbral sonoro de 60 dB, con lo que no detecta ningún sonido por debajo de este nivel sonoro. ¿A qué intensidad corresponde este nivel sonoro? ¿A qué distancia empezará a detectar el sonido si la sirena emite de manera uniforme en una semiesfera? Datos: intensidad umbral de audición: 10-12 W/m2. |
a) Explique en qué consisten las cualidades (intensidad, tono y timbre) de una onda sonora y con qué propiedad física de las ondas están relacionadas.
La primera cuerda de una guitarra (Mi) vibra a 329,63 Hz en el modo fundamental. La cuerda tiene una longitud L = 75 cm.
b) Calcula la velocidad de propagación de las ondas en la cuerda.
c) ¿A qué distancia de uno de los extremos se debe presionar la cuerda para producir la nota Sol, de frecuencia 392 Hz?
a) La intensidad del sonido puede medirse en decibelios (dB). Explica en qué consiste la escala decibélica de intensidad acústica (o sonoridad). El nivel de intensidad sonora de la sirena de un barco es de 60 dB a 10 m de distancia. Suponiendo que la sirena es un foco emisor puntual, calcula: b) El nivel de intensidad sonora a 1 km de distancia. c) La distancia a la que la sirena deja de ser audible. Dato: I0 = 10-12 W/m2 |
a) La intensidad del sonido puede medirse en decibelios (dB). Explica en qué consiste la escala decibélica de intensidad acústica (o sonoridad). Un agente secreto está grabando con un teléfono móvil, a través de una pared, una conversación de un espía enemigo. La distancia entre ambos es de 5 m y, debido a la pared, al teléfono sólo le llega un 2% de la intensidad que le llegaría si no hubiera pared. El nivel de intensidad sonora de una conversación a 1 m es de 50 dB. b) Calcula el nivel de intensidad sonora que llega al móvil. Si el teléfono es capaz de grabar conversaciones a 100 metros de distancia, ¿cuál es el nivel más bajo de intensidad sonora que es capaz de medir?
Dato: Intensidad umbral del oído humano Io = 10−12 W/m2. |
Una fuente sonora puntual emite con una potencia de 10-6 W. a) Determina el nivel de intensidad expresado en decibelios a 1 m de la fuente sonora. b) ¿A qué distancia de la fuente sonora el nivel de intensidad se ha reducido a la mitad del valor anterior? Dato: La intensidad umbral del oído humano es Io = 10-12 W/m2. |
El umbral de dolor sonoro para el oído humano es de 120 decibelios (dB). a) Define el concepto de decibelio. b) ¿A qué intensidad sonora, medida en W/m2, corresponde el valor de 120 dB? c) Si el motor de un avión a reacción emite una potencia de 106 W distribuida por igual en todas las direcciones del espacio, ¿a qué distancia mínima debemos situarnos para no sentir dolor en los oídos? |
a) Un tubo de longitud L = 34 cm tiene uno de los extremos abierto a la atmósfera y el otro extremo cerrado. Calcula la menor frecuencia de excitación sonora para la que se formará una onda estacionaria en el interior del tubo. b) ¿Cuál sería su frecuencia si suponemos ahora que el tubo tiene sus dos extremos abiertos a la atmósfera? Dato: Velocidad de propagación del sonido en el aire v = 340 m/s. |
Se pretende afinar una guitarra eléctrica en “Re vago” de forma que en la sexta cuerda suene un Re, cuya frecuencia es 293,66 Hz. La longitud de la cuerda es de 79 cm. Si Re es el armónico fundamental, a) ¿A qué velocidad se desplazarán las ondas viajeras en la cuerda? b) ¿Qué frecuencia tendrá el siguiente armónico? ¿A qué tensión deberá estar sometida la cuerda si su densidad lineal es de 3,99·10-4 kg/m? |
a) Se desea fabricar un instrumento musical de viento con una tubería de PVC. Para ello se corta la tubería en trozos de distintos tamaños con los dos extremos abiertos. Si el primer trozo tiene una longitud de 25 cm, calcule la frecuencia del armónico fundamental que producirá. ¿De qué tamaño habrá que cortar el siguiente trozo para que produzca una onda estacionaria cuya frecuencia del armónico fundamental sea 2/3 de la frecuencia del armónico fundamental del primer tubo? Dé la longitud de onda de ambos sonidos. Datos: Velocidad del sonido en el aire: 346 m/s. |
a) Explique el fenómeno de interferencia entre dos ondas.
Por una cuerda tensa se propagan dos ondas armónicas y1(x,t) = +0,02·sen(2πt + 20πx) e y2(x,t) = -0,02·sen(2πt - 20πx) (expresadas en unidades S.I.). La interferencia de ambas produce una onda estacionaria
b) Determine la ecuación de la onda estacionaria resultante.
c) Calcule la distancia entre dos nodos consecutivos
Dato: senα – senβ = 2 sen [(α – β)/2] cos[(α + β)/2]
|
|
Enuncia el Principio de Huygens y, a partir de él, demuestra las leyes de reflexión y refracción para una onda que incide sobre una superficie plana de separación entre dos medios, en los que la onda se propaga con diferentes velocidades v1 y v2.
Una onda de frecuencia f = 4 Hz. se propaga por un medio con velocidad v1 = 2 m/s e incide sobre la frontera con otro medio diferente con ángulo de incidencia e =30º. En el segundo medio la velocidad de propagación de la onda es v2 = 2,5 m/s. Calcula el ángulo de refracción y la longitud de onda en ese segundo medio.
Datos: Velocidad del sonido: en el aire, vaire = 340 m/s; en el vidrio, vvidrio = 5770 m/s |
|
|
|
a) Determine la amplitud de la onda, su longitud de onda y la velocidad de propagación de la onda. b) Calcule la máxima velocidad de oscilación transversal de los puntos de la cuerda. c) Escriba la función de onda correspondiente, en unidades S.I. |
Por una cuerda tensa se propaga, en el sentido positivo del eje x, una onda armónica transversal. Los puntos de la cuerda oscilan con una frecuencia f = 4 Hz. En la gráfica se representa la posición de los puntos de la cuerda en el instante t = 0. a) Determine la longitud de onda y la velocidad de propagación de la onda. b) Escriba la función de onda correspondiente, en unidades S.I. c) Calcule la máxima velocidad de oscilación trasversal de los puntos de la cuerda.
|
Una onda transversal se propaga de izquierda a derecha, según el eje OX, a lo largo de una cuerda horizontal tensa e indefinida, siendo su longitud de onda λ = 10 cm. La onda está generada por un oscilador que vibra, en la dirección del eje OY, con un movimiento armónico simple de frecuencia f = 100 Hz y amplitud A = 5 cm. En el instante inicial t = 0, el punto x = 0 de la cuerda tiene elongación nula. a) Escribir una expresión matemática de la onda indicando el valor numérico de todos los parámetros (en unidades S.I.). Escribir la ecuación que describe el movimiento de un punto situado a 30 cm a la derecha del origen. b) Determinar la velocidad de propagación de la onda y la velocidad máxima de oscilación de un punto cualquiera de la cuerda. c) Dibujar un esquema de la cuerda en una longitud de 20 cm, en el instante t = 0 |
 La partícula de masa m = 10 g de la figura 1.a describe el movimiento armónico simple en torno a su posición de equilibrio representado en la figura 1.b (rozamiento despreciable).
|
Un péndulo simple está formado por un hilo de longitud L = 99,2 cm y una bolita que oscila en horizontal con una amplitud A = 6,4 cm y un periodo T = 2,00 s.
|
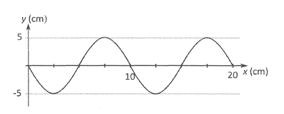
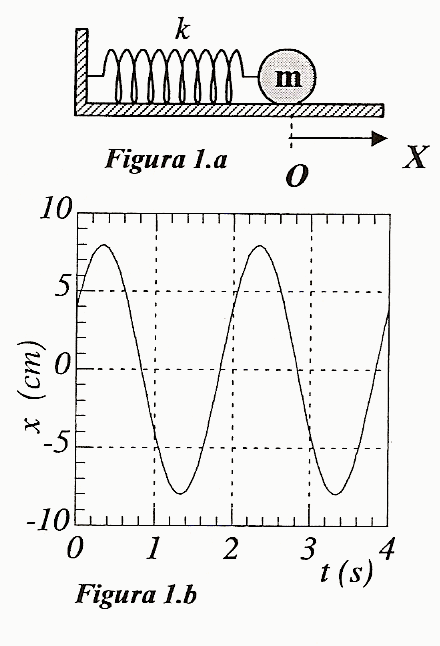
 Una partícula de masa m = 20 g. Oscila armónicamente en la forma x(t) = A sen ωt. En la figura se representa la velocidad de la partícula en función del tiempo.
|
Se dispone de un péndulo simple de 87 cm de longitud que oscila respecto a su posición de equilibrio con un ángulo muy pequeño. Obtenga la frecuencia angular de oscilación y el periodo. Escriba la ecuación de la posición en función del tiempo si la amplitud inicial es de A = 2 cm y x(t = 0 s) = A. ¿Cuál es la velocidad del péndulo al pasar por la vertical?
Datos: Aceleración de la gravedad: 9,8 m/s2.
|
Escribe la ecuación de la elongación de un movimiento vibratorio armónico simple y comenta el significado físico de las magnitudes que aparecen en dicha ecuación.
Un bloque de masa M = 0,4 kg desliza sobre una superficie horizontal sin rozamiento con velocidad v0 = 0,5 m/s. El bloque choca con un muelle horizontal de constante elástica k = 10 N/m. Tras el choque, M se queda enganchada en el extremo del muelle.
Calcula la frecuencia y la amplitud de las oscilaciones de M.
Determina y representa gráficamente la posición del centro de M en función del tiempo, x(t), a partir del instante del choque (t =0), en el sistema de referencia indicado en la figura.
Una partícula de masa m = 0,1 kg oscila armónicamente en la forma x = A sen ω t, con amplitud A = 0,2 m y frecuencia angular ω= 2 π rad/s.
Calcular la energía mecánica de la partícula.
Determina y representa gráficamente las energías potencial y cinética de m en función de la elongación x
Se tiene una masa de 2 kg oscilando verticalmente en un muelle de constante elástica 50 N/m. a) Obtén el periodo de la oscilación. b) Si la velocidad máxima es de 37 cm/s, ¿Cuál es la amplitud máxima de la oscilación? c) Si el muelle se estira hasta el punto más bajo y se suelta, dibuja un gráfico de la posición en función del tiempo. |
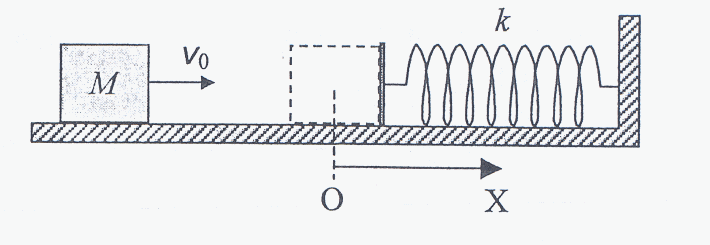
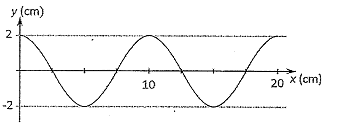
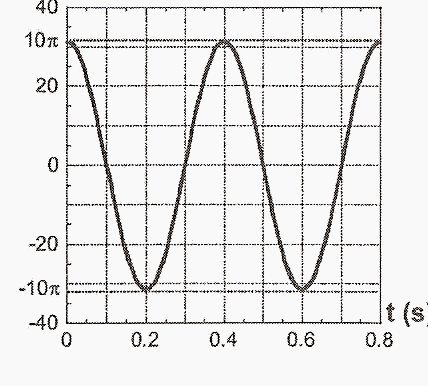
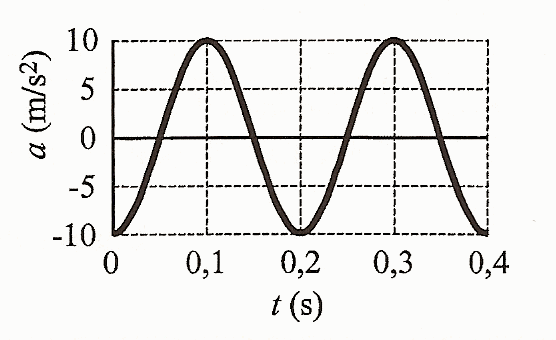Un cuerpo de masa M = 0,1 kg oscila armónicamente en torno al origen O de un eje OX. En la figura se representa la aceleración de M en función del tiempo