S20A

 

a)     Explica el concepto de potencial eléctrico. Superficies equipotenciales.  En una región del espacio existe un campo eléctrico uniforme E = 1000 N/C. En un punto P de esta región, donde supondremos que el potencial eléctrico es nulo, V(P) = 0, liberamos una partícula alfa (He++) con velocidad inicial nula. Una vez que ha recorrido una distancia d = 10 cm:  b)     Calcula su energía potencial en el punto d. c)      Obtén su velocidad.  Datos: carga partícula alfa = 3,2·10-19 C; masa partícula alfa m = 6,64·10-27 kg

J23O

 

Una partícula de masa m = 3,2 × 10-15 kg y cargada con q = 3 mC es acelerada desde el reposo haciendo uso de un campo electrostático uniforme de E1 = 325 V/m a lo largo de 3 metros. a)            ¿A qué velocidad saldrá la partícula del campo electrostático? b)           Seguidamente, entra en otro campo electrostático de magnitud E2 = 125 V/m y sentido opuesto al primero. ¿Cuánta distancia recorrerá hasta detenerse? c)             Describe la expresión de la fuerza electrostática entre dos cargas puntuales y explica sus magnitudes y unidades.

MADRID. 2010 JUNIO FASE GENERAL B. PROBLEMA 2

Tres cargas puntuales de valores q1 = +3 nC, q2= -5 nC y q3 = +4 nC están situadas, respectivamente, en los puntos de coordenadas (0,3), (4,3) y (4,0) del plano XY. Si las coordenadas están expresadas en metros, determine: 

a) La intensidad de campo eléctrico resultante en el origen de coordenadas. 

b) El potencial eléctrico en el origen de coordenadas. 

c) La fuerza ejercida sobre una carga q = 1 nC que se sitúa en el origen de coordenadas. 

d) La energía potencial electrostática del sistema formado por las tres cargas q1, q2 y q3. 

Dato: Constante de la ley de Coulomb: K = 9x109 N m2 C -2

J07B

 

Dos pequeñas esferas, de masa m = 5 g y con carga q, cada una, se suspenden del mismo punto mediante hilos iguales, de masa despreciable y longitud L = 0,5 m, en presencia del campo gravitatorio terrestre. ¿Cuál debe ser el valor de la carga q para que, en equilibrio, los hilos formen un ángulo α = 60º?. Considera g = 10 N/kg ; K = 9·109 N·m²/C²

MADRID 2024 MODELO A3

Dos cargas de 2 nC cada una están fijas en los puntos (0, 0) m y (4, 0) m del plano xy. 

a) Determine el valor de una carga Q si para traerla desde el infinito hasta el punto (2, 2) m el campo hace un trabajo de 1,27·10-7 J. 

b) Indique el punto donde habría que colocar una carga de -10 nC para que la fuerza neta sobre la carga Q fuese cero. 

Dato: Constante de la ley de Coulomb, K = 9·109 N m2 C-2 .

J22E

 

a) Explica el concepto de energía potencial eléctrica. ¿Qué energía potencial eléctrica tiene una partícula de carga q2 situada a una distancia r de otra carga q1? b) Una partícula de carga q1 = 0,1 μC está fija en el vacío. Se sitúa una segunda partícula de carga q2 = 0,5 μC y masa m = 0,1 g a una distancia r = 10 cm de la primera. Si se suelta q2 con velocidad inicial nula, se moverá alejándose de q1. ¿Por qué? Calcula su velocidad cuando pasa por un punto a una distancia 3r de q1.   Datos: Constante de Coulomb: K = 9 x 109 N·m2·C-2

MADRID 2025 JUNIO COINCIDENTES

 3.A. Sean dos cargas puntuales fijas q1 = 1 μC y q2 de valor desconocido situadas en los puntos (- 2, 0) m y (4, 0) m, respectivamente. 

a) Determine el valor de la carga q2 sabiendo que el campo eléctrico generado por ambas cargas en el punto (0, 2) m únicamente tiene componente según el eje x. 

b) Calcule el campo eléctrico total en el punto (0, 2) m. 

c) Si la carga q2 se deja libre, calcule la velocidad que llevará cuando pase por el origen de coordenadas, si su masa es de 1 g. 

Dato: Constante de la ley de Coulomb, K = 9·109 N m2 C−2 .

J23E

 

Se tienen tres partículas cargadas con +2 mC cada una en los vértices 1, 2 y 3 de un triángulo rectángulo, tal y como se muestra en la figura. a)     Calcula la fuerza electrostática total (módulo y ángulo) que hacen las partículas 1 y 2 sobre la partícula 3. b)     Calcula (módulo y ángulo) y dibuja el campo electrostático que crea la partícula 3 en el punto 4, situado en el punto (2cm, 3 cm). c)      Explica el concepto de campo electrostático y da la expresión del campo creado por una carga puntual +q a una distancia r.

J240

 

Contesta a las siguientes preguntas: a)            Explica el concepto de campo eléctrico y da la expresión del campo electrostático producido por una carga puntual q a una distancia r. b)           Calcula el vector campo electrostático producido por el sistema de cargas de la figura en el origen de coordenadas. Datos: constante de Coulomb: K = 9·109 N·m2/C2

J21O

 

a)            Escribe y comenta la Ley de Coulomb. Dos pequeñas esferas, de masa m = 5 g y con carga q, cada una, se suspenden del mismo punto mediante hilos iguales, de masa despreciable y longitud L = 0,5 m, en presencia del campo gravitatorio terrestre. b)           ¿Cuál debe ser el valor de la carga q para que, en equilibrio, los hilos formen un ángulo  α = 90º? Datos: g = 9,8 m/s2, K = 9 x 109 N·m²/C²

MADRID. 2025 JULIO

2.A. Una nave alienígena se sitúa en una órbita circular de radio r en torno a la Tierra. Los tripulantes de la nave observan que tardan 1,59 horas en dar una vuelta completa y saben que la velocidad de escape desde la órbita es 10,7 km s−1 . 

a) Deduzca las expresiones del periodo de la órbita de la nave y de la velocidad de escape desde la órbita en función de G, de la masa de la tierra MT, y del radio de la órbita r. 

b) Calcule el radio de la órbita de la nave y la masa de la Tierra. 

Dato: Constante de Gravitación Universal, G = 6,67·10−11 N m2 kg−2 . 

__________________________________________________________________

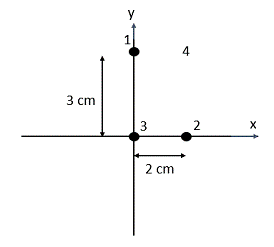
2.B. Sean dos partículas idénticas de masas m1 = m2 = 3 kg, situadas en los puntos P1(0, 0) m y P2(6, 0) m del plano xy. 

a) Halle el campo gravitatorio creado por ambas partículas en el punto (3, 3) m. 

b) Calcule el trabajo que realiza la fuerza gravitatoria para llevar una partícula de masa m = 1 kg desde el punto (3, 3) m al punto (0, 3) m. 

Dato: Constante de Gravitación Universal, G = 6,67·10−11 N m2 kg−2 .

MADRID 2026-Modelo 2.A.

Consideremos el planeta extrasolar G-876d, que tiene una masa igual a 6 veces la masa de la Tierra y un radio de 1,73 veces el radio de la Tierra. El planeta describe una órbita circular de radio 3,14·106 km en torno a la estrella Gliese, cuya masa es de 6,37·1029 kg. Determine: 

a) La aceleración de la gravedad en la superficie del planeta. 

b) La velocidad del planeta en la órbita y su periodo de revolución. 

c) La energía del planeta en la órbita. 

Datos: Constante de la Gravitación Universal, G = 6,67·10−11 N m2 kg−2; Masa de la Tierra, MT = 5,97·1024 kg; Radio de la Tierra, RT = 6,37·106 m

MADRID. JULIO 2023

MADRID 2017. JUNIO COINCIDENTES. B PREGUNTA 1

Considérese una masa M = 50 kg situada en el origen de coordenadas. Bajo la acción del campo gravitatorio creado por dicha masa, determine: 

a) El trabajo requerido para mover una masa m1 = 2 kg desde P1 = (1, 0, 0) m a P2 = (3, 4, 0) m. 

b) La energía cinética de una partícula de masa m2 = 3 kg que, partiendo del reposo, se mueve desde el punto P3 = (9/2, 6, 0) m al punto P2. 

Dato: Constante de Gravitación Universal, G = 6,67·10-11 N m2 kg-2 .

MADRID 2014. SEPTIEMBRE A. PREGUNTA 1.

 3. Un satélite describe una órbita circular alrededor de un planeta desconocido con un periodo de

24 h. La aceleración de la gravedad en la superficie del planeta es 3,71 m·s

-2

y su radio es

3393 km. Determine:

a. EI radio de la órbita. (1 PUNTO)

b. La velocidad de escape desde la superficie del planeta. (1 PUNTO)

Dato: Constante de gravitación universal, G = 6,67×10-11 N m2

kg-2.

REPASO GRAVITACIÓN

 REPASO GRAVITACIÓN

TEORÍAGRAVITACIÓN

S20B

 

a)     Deduce razonadamente la expresión de la velocidad de escape de un planeta de radio R y masa M. b)     Calcula la velocidad de escape del planeta enano Ceres, considerando su forma aproximadamente esférica, si sabemos que su radio es 469,7 km y su densidad media es de 2077 kg/m3. Dato: G = 6,67·10−11 N m2 kg−2.

O21B

 

a) Explica el concepto de campo gravitatorio. Un satélite artificial con una masa de 5000 kg está en órbita circular alrededor de la Tierra con una velocidad orbital de 7563 m/s. Calcular: b) La altura de la órbita sobre la superficie terrestre y su periodo de revolución. c) La energía que tendría que ganar para salir del campo gravitatorio terrestre. Datos: G = 6,67 x 10-11 N·m2·kg-2; MTierra = 5.97 x 1024 kg; RTierra = 6,37 x 106 m

O24A

 

El planeta Marte tiene dos satélites naturales, Fobos y Deimos. El radio orbital de Fobos es de 12767 km, a)     Obtén el periodo orbital de Fobos. b)     Utiliza la tercera ley de Kepler para obtener el periodo orbital de Deimos, cuyo radio orbital es de 26950 km. c)      Calcula la velocidad de escape de un cohete desde la superficie de Fobos, suponiendo que el satélite es esférico. Datos: masa de Marte: MMarte = 6,39·1023 kg, radio de Fobos: RFobos= 21 km, masa de Fobos: MFobos = 1,08·1016 kg, constante de gravitación universal: G = 6,67·10-11 N·m2/kg2.

E23A

 

Un satélite de 80 kg se encuentra en órbita circular alrededor de la Tierra a una altura de 586 km sobre la superficie. a)     Calcula el campo gravitatorio de la Tierra a dicha altura y la Energía del satélite. b)     ¿Cuál es el periodo de la órbita del satélite alrededor de la Tierra? c)      Explica el concepto de Energía potencial gravitatoria y da su expresión para una masa m que orbita a una distancia r de otra masa M. Datos: Radio de la Tierra: 6370 km, cte. de Gravitación universal: 6,67 × 10-11 N m2/kg2, Masa de la Tierra: 5,972 × 1024 kg.

E24A

 

El satélite meteorológico Flexible Combined Imager, con una masa de 2000 kg, fue lanzado por la Agencia Europea del Espacio el 13 de diciembre de 2022 y está revolucionando la predicción meteorológica en Europa. a)     ¿Qué energía hubo que transmitirle para ponerlo en órbita circular a una altitud de 36.000 km, despreciando la energía cinética inicial? b)     ¿Cuáles serán su velocidad y su periodo una vez en órbita? Datos: constante de gravitación universal: G = 6,67·10-11 N·m2/kg2, radio de la Tierra: RT = 6370 km, masa de la Tierra: MT = 5,972·1024 kg.

E22A

 

a) Enuncia y explica la ley de gravitación universal. La luna es aproximadamente esférica, con radio R = 1,74 x 106 m y masa M = 7,35 x 1022 kg. b) Calcula la aceleración de la gravedad en la superficie de la Luna. c) Si se deja caer una piedra desde una altura de 1 m sobre la superficie lunar, ¿cuál será su velocidad al chocar con la superficie? Datos: G = 6,67 x 10-11 N·m2·kg-2

S13A

 

a)      Explicar el concepto de energía potencial gravitatoria. ¿Qué energía potencial gravitatoria tiene una partícula de masa m situada a una distancia r de otra partícula de masa M? b)      En el libro de Julio Verne “De la Tierra a la Luna” tres hombres viajan a la Luna en un cohete disparado desde un cañón gigante situado en Florida. Calcular la velocidad inicial con la que hay que disparar el cohete verticalmente para que alcance una altura sobre la superficie de la Tierra igual a 9 veces el radio de ésta. ¿Qué energía potencial gravitatoria tendrá el cohete cuando llegue a ese punto? Datos: G = 6,67·10-11 Nm2 kg-2 ; MT = 5,97 1024 kg ; RT = 6,38 ·106 m. Masa cohete, m = 5·103 kg

J14B

 

a)      Explicar el concepto de energía potencial gravitatoria. ¿Qué energía potencial gravitatoria tiene una partícula de masa m situada a una distancia r de otra partícula de masa M? b)      Desde la superficie de un planeta esférico sin atmósfera, de masa M y radio R, se lanza verticalmente un proyectil que llega a alcanzar una altura máxima de h = R/2 antes de caer a su superficie. ¿Con qué velocidad inicial se ha lanzado el proyectil?.   Datos: G = 6,67·10-11 Nm2 kg-2 ; M = 1,5 1023 kg ; R = 1,6 ·106 m.

J01B

 

1. Explica el concepto de campo gravitatorio creado por una o varias partículas.

2. Dos partículas de masas M₁ y M₂ = 4 M₁   están separadas una distancia d = 3 m. En el punto P, situado entre ellas, el campo gravitatorio total creado por estas partículas es nulo. Calcula la distancia x entre P y M1.

J05A

 

Explica el concepto de campo gravitatorio creado por una o varias partículas. La Tierra es aproximadamente esférica, de radio RT = 6,37·106 m. La intensidad media del campo gravitatorio en su superficie es go = 9,81 m/s2. Calcula la densidad de masa media de la Tierra. ¿A qué altura h sobre la superficie de la Tierra se reduce g a la cuarta parte de go? G = 6,67·10-11 N m2 kg-2

J17B

a)      Enuncie y explique la ley de gravitación universal. La nave Apolo 11 permitió la llegada del hombre a la Luna en 1969. Para ello orbitó alrededor de ella con un periodo de 119 minutos y a una distancia media del centro de la Luna de 1850 km. Suponiendo que su órbita fue circular, determine: b)      La velocidad orbital del Apolo 11. c)      La masa de la Luna. Datos: Constante de gravitación universal, G = 6,67-10-11 NI-m2-kg-2.