GRAVITACIÓN UNIVERSAL
J96B En los Juegos Olímpicos del año terrestre 2124 celebrados en Marte, un
atleta marciano obtiene la medalla de oro en salto de altura al superar el listón
colocado a 5,75 m.
a. Calcula la gravedad en Marte.
b. Si las pruebas olímpicas se hubieran realizado en la Tierra, calcula la
altura que hubiera podido saltar el atleta marciano.
Datos: Constante gravitación Universal, G = 6,67·10-11 U.S.I., masa de Marte,
M=6,50·1023 Kg, radio de Marte, R = 3400 km., gravedad en la superficie de la
Tierra, go = 9,81 m/s²
J00B
a. La intensidad media del campo gravitatorio en la superficie de la Tierra es
g = 9,81 N/kg. Calcula la masa de la Tierra.
b. ¿A qué altura sobre la superficie se reduce g a la mitad del valor indicado?
Datos: RT = 6,37·106 m.; G = 6,67·10-11 N·m²/kg²
J01B
a. Explica el concepto de campo gravitatorio creado
por una o varias partículas.
b. Dos partículas de masas M1 y M2 = 4 M1 están
separadas una distancia d = 3 m. En el punto P,
situado entre ellas, el campo gravitatorio total
creado por estas partículas es nulo. Calcula la
distancia x entre P y M1.
J02B
a. Calcula la intensidad del campo gravitatorio, gJ, en la superficie de Júpiter.
¿A qué altura sobre la superficie de Júpiter, h, se reduce g al valor
superficial terrestre de 9,81 N/kg?
G = 6,67·10-11 N m2 kg-2
; MJ = 1,90.1027 kg; RJ = 6,98.107 m.
b. El periodo de oscilación de un péndulo simple en la 'superficie de la Tierra
es T = 1,2 s. ¿Cuál sería su periodo de oscilación en la superficie de
Júpiter?
S03A
a. Explica el concepto de campo
gravitatorio creado por una o varias partículas.
b. La distancia entre los centros de la Tierra y la
Luna es d = 3,84·108 m. En cierto punto P,
situado entre ambas, el campo gravitatorio es nulo. Sabiendo que la masa
de la Tierra es 81 veces superior a la de la Luna, calcula la
distancia x entre P y el centro de la Luna.
S04B
a. Escribe y comenta la Ley de Gravitación Universal.
b. Se deja caer un cuerpo desde una altura h = 2 m sobre la superficie de la
Luna. Calcula su velocidad cuando choca con la superficie y el tiempo de
caída.
G = 6,67·10-11 N m2 kg-2
; Masa y Radio de la Luna, ML = 7,34·1022 kg, RL =
1,74·106 m
J05A
a. Explica el concepto de campo gravitatorio creado por una o varias
partículas.
La Tierra es aproximadamente esférica, de radio RT = 6,37·106 m. La intensidad
media del campo gravitatorio en su superficie es go = 9,81 m/s2
.
b. Calcula la densidad de masa media de la Tierra.
c. ¿A qué altura h sobre la superficie de la Tierra se reduce g a la cuarta
parte de go?
G = 6,67·10-11 N m2 kg-2
S06B
a. Escribe y comenta la Ley de Gravitación Universal
b. Dos planetas esféricos tienen la misma masa, M1 = M2, pero la
aceleración de la gravedad en . superficie del primero es cuatro veces
mayor que en la del segundo, g1 = 4·g2. Calcula la relación entre los radios
de los dos planetas, R1/R2, y entre sus densidades medias de masa, ρ1/ρ2.
J08B
a. Explica el concepto de campo gravitatorio creado por una o varias
partículas
b. Consideremos la Tierra y
la Luna aproximadamente
esféricas, de radios RT =
6,38·106 m y RL =
1,74·106 m. La distancia
entre los centros de la Tierra y la Luna es d = 3,84·108 m.
Compara el valor de la intensidad de campo gravitatorio en el punto P de la
superficie lunar, situado en la línea que une el centro de la Luna con el de la
Tierra, creado por la Luna, con el valor, en ese mismo punto, del campo creado
por la Tierra.
Datos: G = 6,67·10-11 N·m²·kg-2
; MT = 5,97·1024 kg ; ML = 7,35·1022 kg
J09A
a. Escribe y comenta la Ley de Gravitación Universal.
b. El satélite meteorológico SMOS (Soil moisture and ocean salinity) de
masa 683 kg se pretende colocar en órbita circular (polar) a una altura h =
755 km sobre la superficie terrestre.
1. Calcula la variación que experimentará el peso del satélite en la órbita,
respecto al que tiene en la superficie terrestre.
2. Determina la velocidad orbital del satélite y el número de veces que recorrerá
la órbita cada día.
Datos: G = 6,67·10-11 N·m²·kg-2
; MT = 5,97·1024 kg ; RT = 6,38·106 m
S11A
a) Escribe y comenta la Ley de Gravitación Universal
b) Calcula la intensidad de campo gravitatorio gM en la superficie de Marte.
¿A qué altura sobre la superficie de la Tierra coincide el valor de la intensidad
del campo gravitatorio terrestre g con la gM calculada para la superficie de
Marte?
Datos: G = 6,67·10-11 N·m2
·kg-2.; MTierra = 5,97·1024 kg; MMarte =
6,42·1023 kg, RTierra = 6,38·106 m; RMarte = 3,40·106 m,
S15A
a) Explique el concepto de campo gravitatorio creado por una o varias
partículas.
b) La intensidad del campo gravitatorio de la Tierra a nivel del mar es g0 =
9,81 m/s2
. Calcule el valor en lo alto del Everest, de 8850 m de altitud sobre
el nivel del mar.
c) Si lanzamos desde la cima del Everest un proyectil en dirección
perpendicular al radio terrestre, ¿cuál debe ser su velocidad para que
describa una órbita circular alrededor de la Tierra? (Desprecie los efectos del
rozamiento con la atmósfera).
Datos: Radio de la Tierra, RT = 6,38·106 m
S18B
a) Enuncie y comente la Ley de Gravitación Universal.
Caronte es un satélite que orbita alrededor de Plutón con una órbita
prácticamente circular de periodo 6,39 días.
b) A partir de los datos de Caronte y Plutón, calcule la masa de Plutón.
c) Calcule el campo gravitatorio (módulo, dirección y sentido) en el punto
medio de la línea que une los centros de Caronte y Plutón.
Datos: Constante de gravitación universal, G=6,67∙10-11N∙m2
∙kg-2; masa de Caronte, MC=1,52∙1021 kg; distancia Plutón-Caronte, r = 19570 km
LEY DE LORENZ.
a) Escriba la expresión de la Fuerza de Lorentz que actúa sobre una
partícula de carga q que se mueve con velocidad en una región
donde hay un campo magnético . Explique las características de esta
fuerza.
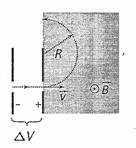
Un protón que lleva una velocidad de 1,00·105 m/s según el sentido
positivo del eje X entra en un espectrómetro de masas en el que hay un
campo magnético
b) Calcule la fuerza (módulo, dirección y sentido) que actúa sobre el
protón. Determine el radio de su trayectoria.
c) Calcule el campo magnético (módulo, dirección y sentido) necesario
para que, si entra un electrón con la misma velocidad que el protón en
el espectrómetro, describa la misma trayectoria.
Datos: k = 1/(4πε0) = 9,0 x 109 N·m2·C-2; carga del protón qp=1,60 x
10-19 C; carga del electrón qe= -1,60 x 10-19 C; masa del electrón
me=9,11 x 10-31 kg; masa del protón mp=1,67 x 10-27 kg
CONDUCTORES PARALELOS, CAMPO Y FUERZA ENTRE ELLOS
Dos conductores rectilíneos, verticales y paralelos, A a la izquierda y B a
la derecha, distan entre sí 20 cm. Por A circula una corriente IA = 10 A
hacia arriba. El campo magnético en un punto situado a 8 cm a la
izquierda de A es nulo.
a) Calcule la intensidad de corriente que circula por B. ¿En qué sentido
circula?
b) Explique con ayuda de un esquema si hay algún punto entre los
dos conductores donde el campo magnético sea nulo
c) Calcule la fuerza por unidad de longitud que un conductor A ejerce
sobre el B. Indique su dirección y sentido
Datos: μ0 = 4π·10-7 m·kg·C-2
1. Dos conductores rectilíneos de gran longitud, verticales y paralelos,
están separados una distancia de 50 cm. Si por ellos circulan corrientes
iguales de 12 A de intensidad y sentidos opuestos, calcula el módulo del
campo magnético resultante en los siguientes puntos:
a) Punto P equidistante a ambos conductores.
b) Punto Q situado a 50 cm de un conductor y a 100 cm del otro.
Dato: μ0 = 4π·10-7 T m/A
 crea en su entorno una corriente eléctrica rectilínea e indefinida? Explica cómo son, y dibuja, las líneas de campo magnético. ¿Cómo cambian los resultados anteriores al invertir el sentido de la corriente?
crea en su entorno una corriente eléctrica rectilínea e indefinida? Explica cómo son, y dibuja, las líneas de campo magnético. ¿Cómo cambian los resultados anteriores al invertir el sentido de la corriente?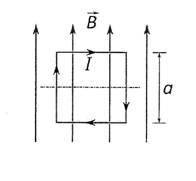 Enuncie y explique las leyes de Faraday y Lenz sobre inducción electromagnética.
Enuncie y explique las leyes de Faraday y Lenz sobre inducción electromagnética.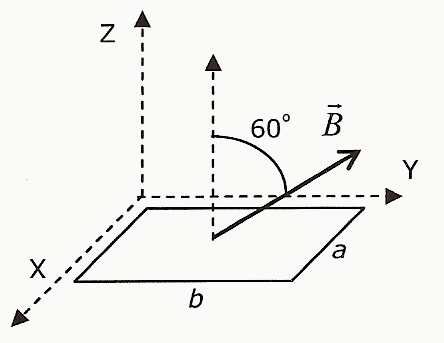
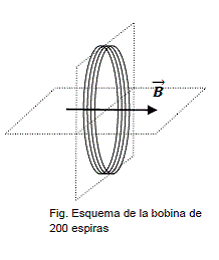 Disponemos de una bobina circular de N = 200 espiras y radio R = 0,2 m. Atraviesa dicha bobina un campo magnético B = 0,25 T paralelo a su eje, tal como se muestra en la figura.
Disponemos de una bobina circular de N = 200 espiras y radio R = 0,2 m. Atraviesa dicha bobina un campo magnético B = 0,25 T paralelo a su eje, tal como se muestra en la figura.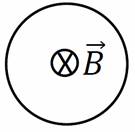
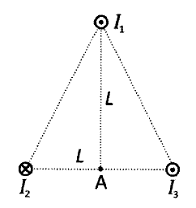 Tres conductores rectilíneos, paralelos y muy largos, colocados en los vértices de un triángulo isósceles de base y altura L = 10 cm, transportan corrientes I1 = 10 A e I3 = 5 A, del mismo sentido, e I2 =5 A de sentido contrario.
Tres conductores rectilíneos, paralelos y muy largos, colocados en los vértices de un triángulo isósceles de base y altura L = 10 cm, transportan corrientes I1 = 10 A e I3 = 5 A, del mismo sentido, e I2 =5 A de sentido contrario.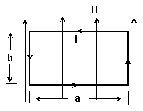 espira y están orientadas como indica la figura.
espira y están orientadas como indica la figura.