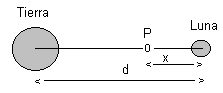El Sol orbita alrededor del centro galáctico siguiendo una órbita circular de radio 2,4 10 ⋅ 17 km y periodo de 203 millones de años. Determine:
a) La velocidad orbital del Sol alrededor del centro galáctico.
b) La masa del centro galáctico suponiendo que toda la masa se concentra en un agujero negro en su centro.
Dato: Constante de Gravitación Universal, G = 6,67·10-11 N m2 kg-2
B.1. En la película Space Cowboys un amenazador satélite militar orbita alrededor de la Tierra a una altura de 1600 km sobre la superficie terrestre.
a) Calcule la velocidad orbital del satélite y el tiempo que tarda en dar una vuelta completa alrededor de la Tierra. Desprecie en este apartado la interacción gravitatoria de la Luna.
b) Para evitar que el satélite caiga a la Tierra
se decide impulsarlo hacia la Luna. Determine
la distancia x al centro de la Tierra, tal y como
se muestra en la figura, a la que tendrá que
llegar el satélite, para que el efecto del campo
gravitatorio lunar sea superior al del campo
gravitatorio terrestre.
Datos: Constante de Gravitación Universal, G = 6,67·10-11 N m2 kg-2; Masa de la Tierra, MT = 5,97·1024 kg; Radio de la Tierra; RT = 6,37·103 km; Masa de la Luna, ML = 7,35·1022 kg; Distancia de la Tierra a la Luna, d = 3,84·105 km.
|
a) Explique el concepto de campo gravitatorio creado por una o varias partículas. b) La intensidad del campo gravitatorio de la Tierra a nivel del mar es g0 = 9,81 m/s2. Calcule el valor en lo alto del Everest, de 8850 m de altitud sobre el nivel del mar. c) Si lanzamos desde la cima del Everest un proyectil en dirección perpendicular al radio terrestre, ¿cuál debe ser su velocidad para que describa una órbita circular alrededor de la Tierra? (Desprecie los efectos del rozamiento con la atmósfera). Datos: Radio de la Tierra, RT = 6,38·106 m |
a) Escriba y comente la Ley de Gravitación Universal. b) La Tierra gira alrededor del Sol con un periodo de un año y un radio medio de 1,50·108 km. Teniendo en cuenta únicamente el sistema formado por el Sol y la Tierra, y considerando la órbita prácticamente circular, calcule la velocidad de traslación de la Tierra y la masa del Sol. c) Si por un cataclismo el radio de la órbita se duplicara, ¿cuál sería el nuevo periodo?. Datos: Constante de gravitación universal, G = 6,67·1011 N·m2·kg-2; masa de la Tierra, MT = 5,97·1024 kg. |
a) Escribe y comenta la ley de Gravitación Universal. La Estación Espacial Internacional (ISS) realiza 15,49 revoluciones por día alrededor de la Tierra. Considerando que sigue una órbita aproximadamente circular: b) ¿A qué altura por encima de la superficie terrestre se encuentra la estación espacial ISS? c) ¿A qué velocidad se desplaza? Datos: G = 6,67 x 10-11 N·m2·kg-2; MTierra = 5.97 x 1024 kg; RTierra = 6371 km |
Galileo observó por primera vez las lunas de Júpiter en 1610. Encontró que Io, el satélite más cercano a Júpiter que pudo observar en su época, poseía un periodo orbital de 1,8 días y el radio de su órbita era, aproximadamente, 3 veces el diámetro de Júpiter. Asimismo, encontró que el periodo orbital de Calisto (la cuarta luna más alejada de Júpiter) era de 16,7 días. Con esos datos, suponiendo órbitas circulares, calcula: a) La masa de Júpiter. b) El radio de la órbita de Calisto. c) Determina el valor de la aceleración de la gravedad en la superficie de Júpiter. |
Escribe y comenta la Ley de Gravitación Universal
Dos planetas esféricos tienen la misma masa, M1 = M2, pero la aceleración de la gravedad en . superficie del primero es cuatro veces mayor que en la del segundo, g1 = 4·g2. Calcula la relación entre los radios de los dos planetas, R1/R2, y entre sus densidades medias de masa, ρ1/ρ2.
a) Escribe y comenta la Ley de Gravitación Universal
b) Calcula la intensidad de campo gravitatorio gM en la superficie de Marte. ¿A qué altura sobre la superficie de la Tierra coincide el valor de la intensidad del campo gravitatorio terrestre g con la gM calculada para la superficie de Marte?
Datos: G = 6,67·10-11 N·m2·kg-2.; MTierra = 5,97·1024 kg; MMarte = 6,42·1023 kg, RTierra = 6,38·106 m; RMarte = 3,40·106 m,
a) Enuncie y explique las leyes de Kepler. b) La Tierra y Venus describen órbitas en torno al Sol, siendo el radio medio de la órbita de Venus 0,72 veces el radio orbital de la Tierra. Suponiendo válida la aproximación de órbitas circulares, calcule la duración del año ‘venusiano’. c) Determine la relación de las velocidades orbitales y el cociente entre los momentos angulares de la Tierra y de Venus, con respecto al centro del Sol. Datos: G = 6,67·10-11 N·m2·kg-2. MTierra = 5,98·1024 kg; MVenus = 4,87·1024 kg, año terrestre = 365 días. |
a) Enuncie y explique las Leyes de Kepler.
b) Las órbitas de dos de los planetas de la estrella Cervantes(1), llamados Quijote y Sancho, tienen radios de 1,54 U.A. y 0,93 U.A. respectivamente. Quijote tarda 646 días en dar una vuelta alrededor de Cervantes. Calcule el periodo orbital de Sancho.
c) Obtenga la relación entre las velocidades orbitales de Quijote y Sancho.
a) Enuncie y explique las Leyes de Kepler. Ío y Calisto son dos satélites que orbitan alrededor de Júpiter. Ío tiene un periodo orbital de 1,8 días y el radio de su órbita es 6 veces el radio de Júpiter. El periodo orbital de Calisto es de 16,7 días. b) Suponiendo que Ío y Calisto describen órbitas circulares, calcule el radio de la órbita de Calisto. Dato: radio de Júpiter, RJ=71500 km. |
