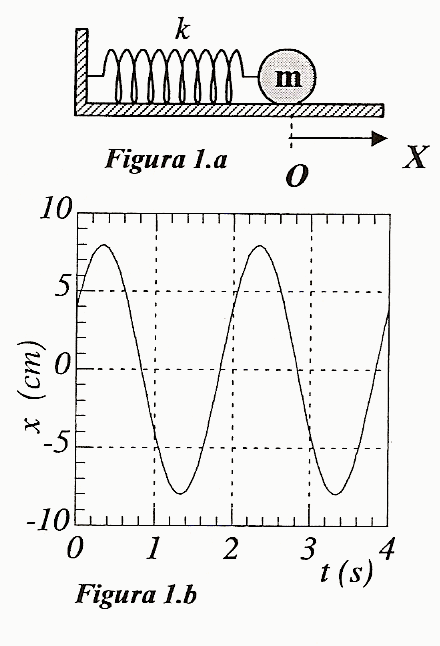 La partícula de masa m = 10 g de la figura 1.a describe el movimiento armónico simple en torno a su posición de equilibrio representado en la figura 1.b (rozamiento despreciable).
|
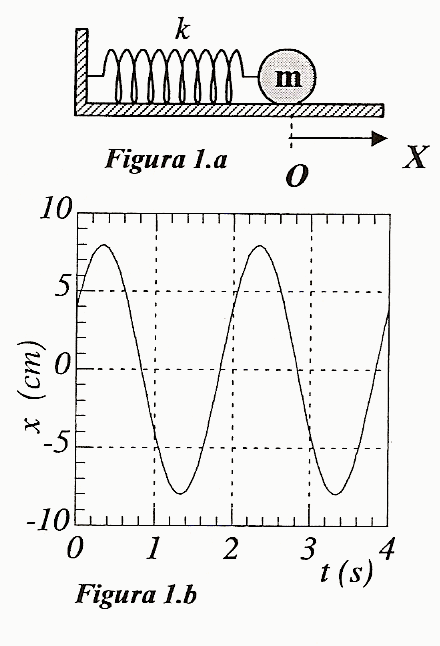 La partícula de masa m = 10 g de la figura 1.a describe el movimiento armónico simple en torno a su posición de equilibrio representado en la figura 1.b (rozamiento despreciable).
|
Un péndulo simple está formado por un hilo de longitud L = 99,2 cm y una bolita que oscila en horizontal con una amplitud A = 6,4 cm y un periodo T = 2,00 s.
|
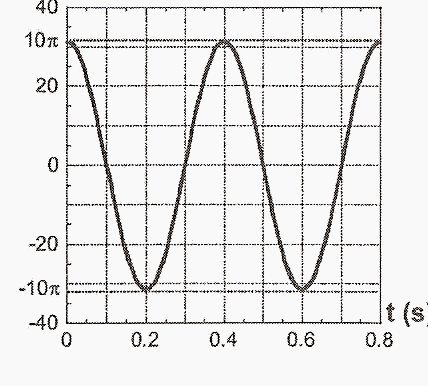 Una partícula de masa m = 20 g. Oscila armónicamente en la forma x(t) = A sen ωt. En la figura se representa la velocidad de la partícula en función del tiempo. Una partícula de masa m = 20 g. Oscila armónicamente en la forma x(t) = A sen ωt. En la figura se representa la velocidad de la partícula en función del tiempo.
|
Se dispone de un péndulo simple de 87 cm de longitud que oscila respecto a su posición de equilibrio con un ángulo muy pequeño. Obtenga la frecuencia angular de oscilación y el periodo. Escriba la ecuación de la posición en función del tiempo si la amplitud inicial es de A = 2 cm y x(t = 0 s) = A. ¿Cuál es la velocidad del péndulo al pasar por la vertical?
Datos: Aceleración de la gravedad: 9,8 m/s2.
|
Escribe la ecuación de la elongación de un movimiento vibratorio armónico simple y comenta el significado físico de las magnitudes que aparecen en dicha ecuación.
Un bloque de masa M = 0,4 kg desliza sobre una superficie horizontal sin rozamiento con velocidad v0 = 0,5 m/s. El bloque choca con un muelle horizontal de constante elástica k = 10 N/m. Tras el choque, M se queda enganchada en el extremo del muelle.
Calcula la frecuencia y la amplitud de las oscilaciones de M.
Determina y representa gráficamente la posición del centro de M en función del tiempo, x(t), a partir del instante del choque (t =0), en el sistema de referencia indicado en la figura.
Una partícula de masa m = 0,1 kg oscila armónicamente en la forma x = A sen ω t, con amplitud A = 0,2 m y frecuencia angular ω= 2 π rad/s.
Calcular la energía mecánica de la partícula.
Determina y representa gráficamente las energías potencial y cinética de m en función de la elongación x
Se tiene una masa de 2 kg oscilando verticalmente en un muelle de constante elástica 50 N/m. a) Obtén el periodo de la oscilación. b) Si la velocidad máxima es de 37 cm/s, ¿Cuál es la amplitud máxima de la oscilación? c) Si el muelle se estira hasta el punto más bajo y se suelta, dibuja un gráfico de la posición en función del tiempo. |
Un método usado para pesar a los astronautas consiste en hacerles oscilar verticalmente sobre un muelle de forma que, conociendo la constante elástica, se puede determinar la masa del astronauta. a) Si el periodo de oscilación del muelle, supuesto ideal, con una silla anclada de 29,7 kg es de 3,5 s, calcula la constante elástica del muelle. b) ¿Cuál será la masa del astronauta sentado en la silla si el periodo de oscilación se duplica al hacerlo oscilar con el astronauta sentado en la silla? |
La expresión de un M.A.S. es x(t)=0,85cos(1,5πt+Φ)m. ¿Cuál es el valor de la fase inicial Φ para que se cumpla que x(1)=0,3 m? Determine el periodo de la oscilación y la velocidad máxima. |
La siguiente ecuación describe un Movimiento Armónico Simple de una masa de 2 kg colgada de un muelle, A(t) =5 sen (14πt – π/2), expresada en milímetros. a) Obtén la frecuencia angular y el periodo de la oscilación. b) ¿En qué momento o momentos del movimiento adquirirá su velocidad máxima? Calcúlala. c) Obtén la energía mecánica del oscilador para el punto en el que la velocidad es máxima. |
Un elefante se balanceaba verticalmente sobre la tela de una araña de forma que describía un M.A.S.. Si el elefante tiene una masa de 2200 kg y realiza una oscilación completa cada 13 s, a) Calcula la constante elástica de la tela de araña. Si el estiramiento máximo es de 80 cm, ¿cuál es la fuerza elástica máxima que sufrirá el elefante? b) Haz un gráfico de posición en función del tiempo, indicando las magnitudes que consideres importantes y sus unidades. |
a) Escribe la ecuación de la elongación de un movimiento vibratorio armónico simple y comenta el significado físico de las magnitudes que aparecen en dicha ecuación. Una partícula de masa m inicia un movimiento armónico simple en el extremo de su trayectoria y le cuesta 0,1 s llegar al centro de ella. Si la distancia entre ambas posiciones es de 20 cm, calcula: b) El periodo del movimiento y la frecuencia angular. c) La ecuación de la posición de la partícula en función del tiempo. Determina la posición de la partícula 1 s después de iniciado el movimiento. |
La expresión de un M.A.S. es x(t)=0,85cos(1,5πt+Φ)m. ¿Cuál es el valor de la fase inicial Φ para que se cumpla que x(1)=0,3 m? Determine el periodo de la oscilación y la velocidad máxima |
Explica qué es el coeficiente de autoinducción de un circuito.
Por un solenoide de autoinducción L = 0,02 H circula una corriente que decrece con el tiempo en la forma I = I0 – α t – β t2, donde I0 es constante, α = 5 A/s y β = 2,5 A/s2. Determina, en función del tiempo, la f.e.m. autoinducida en el solenoide.
 a) Enunciar y explique las leyes de inducción de Faraday y de Lenz.
a) Enunciar y explique las leyes de inducción de Faraday y de Lenz.
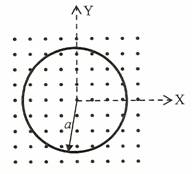
b) Una espira conductora circular, de radio a = 5 cm , está situada en una región donde existe un campo magnético uniforme B = 0,2 k T, dirigido en la dirección del eje Z (perpendicular al plano de la espira y en la figura, con sentido saliente).
b1) Calcular la f.e.m. media inducida en la espira cuando gira 90º en torno al eje Y en un intervalo de tiempo Δt = 0,1 s .
b2) Si la espira permanece fija, pero el campo magnético se duplica en el mismo intervalo de tiempo indicado, ¿cuál es la f.e.m. inducida? Razonar en qué sentido circulará la corriente inducida en la espira.
B.1. Una partícula de masa m se encuentra en el origen de coordenadas de un sistema de referencia (x, y). La componente x del campo gravitatorio creado por la partícula en el punto (2, 2) m es -1,18·10-11 N kg-1.
a) Calcule el valor de la masa m.
b) ¿Cuál es el trabajo que realiza el campo para llevar una partícula de masa M = 5 kg desde el punto (4, 0) m al punto (2, 2) m?
Dato: Constante de Gravitación Universal, G = 6,67·10-11 N m2 kg-2.